Relation between potential energy, potential and force
Potential energy is closely linked with forces. If the work done moving along a path which starts and ends in the same location is zero, then the force is said to be conservative and it is possible to define a numerical value of potential associated with every point in space. A force field can be re-obtained by taking the negative of the vector gradient of the potential field.For example, gravity is a conservative force. The associated potential is the gravitational potential, often denoted by φ or V, corresponding to the energy per unit mass as a function of position. The gravitational potential energy of two particles of mass M and m separated by a distance r is
The work done against gravity by moving an infinitesimal mass from point A with U = a to point B with U = b is (b − a) and the work done going back the other way is (a − b) so that the total work done in moving from A to B and returning to A is
In practical terms, this means that one can set the zero of U and φ anywhere one likes. One may set it to be zero at the surface of the Earth, or may find it more convenient to set zero at infinity (as in the expressions given earlier in this section).



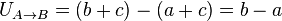
No comments:
Post a Comment